���y�[�p�[���ʎm��
�@���C�ɂ��A���낢��{���̎���m�邱�Ƃ��o����B��������̒m���������ɞB���ł�����
���v���m�鎖�ɂȂ����B
�@���ʎm��̎��i�������Ă���Ƃ����Ă��A�����P�O�N�ȏ�O�ɁA�w������̈��Â��̎���
���ƂقƂ�ƂǓ����v�̂Ŏ��A�K���ɍ��i���Ă��܂��A���܂Ŋo�����m�����قƂ��
���̒����炱�ڂꗎ���Ă��܂����y�[�p�[���ʎm��ł���B
�@�X�ɓy�n�Ɖ������m�����ɍ��i���Ă��܂��ƁA���܂ł̔����Ƃ��艽�����������A�s��
�Y�o�L�@���A���ʂɂ��Ă��A�d���̗���ɐg��C���Ă��܂��B���Ȃ����A������
�����̓s���̗ǂ��悤�ɏ���ɉ��߂��A�y�n�Ɖ������m�ɂ́A�{�i�I�ȑ��ʂȂ�ĕK�v����
���A����ȑ�U���ȑ��ʂȂW�Ȃ��A�ǂ��������m�͏d���̋��������ʂ��ƁA�Ȃɂ�
�ʂȐ��E�̎��̂悤�Ɏv���Ă����B
�@�����ŋ߁A�{���ő��ʎm��W�̎e�L�X�g��ǂ�܂�����蕪����Ȃ��B����͑�
�ς��B�{���Ɏ�������ɉ��߂��Č�������ʂ����Ă���̂ł͂Ȃ��̂��낤���B���������Ύv
�������鎖������B���ʉ�Ђ̑��ʎm�����̎������ɗ��āA�������������ƌ����ė�����
�̂����A���̎��A������Ƒ��ʂ̋Z�p�I�Șb������A�����B���ɑ��Â���łƁA�ɂ�ɂ��
����ċA���čs���B�u�������B����́A�����A���ɂ��m��Ȃ��ȁv�Ɣn���ɂ���Ă����̂�
�͂Ȃ��̂��낤���B�w��₽�����̂�����B
�@����Ȏ��A������Ƃ����������������_���ʂ̌��C��ɎQ�����鎖�ɂȂ�A����o���̒m
�����ǂ�ǂ�ӂ��U���Ă������ɂȂ�B
����_�̎��
�@�܂��A���͍ŋ߂悭���ɂ����_�ɂ��Ă̎�ނ��ǂ����s���Ɨ��Ȃ��B���̒n��͊�
�ɁA���y�������������Ă��邽�߁A�O���O�p�_��l���O�p�_����ɐ}���O�p�_�A�}�����p
�_�ɂ��ẮA�����e����ł���̂����A�P����_�A�Q����_�A�R����_�A�S����_��
��������Ă��A�Ȃ��Ȃ�����Ȃ��B���y�����n��̎��ɗ������₷���悤�ɁA���R�ƂP���
�_�͎l���O�p�_�A�Q����_�͐}���O�p�_�A�S����_�͐}�����p�_�Ƃ������ɗ��������B
�����A�S�R�����͕ʕ��Ƃ������ł���B��_�͌��ݏȍ�ƋK���Ɋ�Â���Ƃ���Ă���A
����������悤�ł���B
�@�X�ɁA���s���̂��ߒm��Ȃ������̂����A�P�A�Q�A�R���O�p�_�͊�{���ʁA�S���O�p�_��
���y�����@�ɂ���{���ʂ���ɍ����_���ʂƌĂԂ̂������ł���B
�@������ƁA�E���B�ׂ�̌��C���Ƃ̖��ʘb�B���̂��߂��S���O�p�_�ɂ��ẮA���y�n���@
�����܂�M�S�ł͂Ȃ��A���������H�H�����ŏ�������Ƃ��ȂǁA�n���@�ɕ������킵�Ă��
���Ă������ł��档�Ƃ������Ԏ������鎖�������Ƃ����B
�����x�E�C���̕
�@�n���̊ۂ��B��X�̑��ʂɂ͈�ԊW�������Ǝv���Ă��������ł���B�����m�ɂƂ��āA��
�E���m�肵�����ɍY����ꌻ�n�����肵�A���̍Y�𑪂����ʐς����������̊�ɂȂ�B�]��
�āA�ʐς�Ӓ��ɂ��Ēn���̊ۂ��Ȃ�čl����K�v�͂Ȃ��B��X�̑��ʂɂ��ẮA����
�ꏊ�ŁA���ۂɑ���ł���ʐςł���A�Ӓ����K�v�ȂA�����畽�ʂƍl���Ă��������A��
�R�ƍl���Ă����B�������A�ǂ̒��x����n���̊ۂ����e������������̂����m��Ȃ������A��
��A�m�肽���Ȃ������B
�@��x�A�^�~�Ɉ�M�n�𑪂������ɓ������r���Ŋϑ��𒆎~���A�����A�lj����ʂ�������
�Ɋm�F�̂��ߓ���_�𑪂����Ƃ��닗�����P�Z���`�߂������������������������A��B�_�A��
���_�����đ��_�Ƃ������e��ݒu���A��Q�����������ʂ����ǂ����ɑ��_�͊�B�_���������
�e���̂��̂�������Ƃ����D�����ł������R�O���[�g�����̋����ł̎��ł���B���������āA��
�g�����V���v���Y�������Ȃ��A�����e�ɂ���������ƃv���Y���������Ă����B���̏؋��Ɋp�x
�͂҂������v����B
�@�V��͗����̕����Q�A�R�x�g��������������قǂ̑���͂Ȃ��B���̂��낤�ƍl����ƁA�O
���͊����čH���̐l�v�����x���̂R�`�S���[�g�����ŕ��������Ă����B���̑��_�͒��x
�����̉���ʂ��ċ����𑪂��ԂɂȂ��Ă���A�u�����A�����̂������B���x�������ɉe
����^����̂��B�v���x�Ƌ����ɂ��āA�������P���Ŏ������Ă��܂����B
�@���̎�����^�~�ƁA�^�Ăœ���n�_�ŒP���ɋ����̑�����s���ƁA���R�قȂ鎖�ɂȂ�B��
����A�ǂ̂悤�ȉ��x�̎��ɋ������ϑ����Ă����x�ɂ�������Ă����A����̋�����
�鎖���o����B
�@���Ȃ݂ɉ��x�������Ȃ�قNj��������Ȗڂɕ\�����鎖�ɂȂ邻���ł���B�Ȃ�ł��P�O�x��
���x�ω�������ƁA���苗���͂P�L���ɂ��Ė�P�Z���`�ω����A�P�O�����g���̋C���ω�����
��ƂP�L���ɂ��Ė�S�����̊����ŕω����邻���ł���B�����́A���g�����V�̒��ɁA����
�̋C���A�C������͂��邾���ŊȒP�ɉ�������B�{�^������������炸���܂߂ɓ��͂��鎖�B
�����e�
�@�X�ɁA��ԉ�X���s���Ɨ��Ȃ����B�n���̊ۂ��ɂ��čl���鎞�A�n���̒��S���牓���Ȃ�
�قǁA�n���̒��S���瓯�S�~��`�����A���S�̊p������̊p�x�ł���A�����Ȃ�قǁA����
�p�x�����鋗���͒����Ȃ�ƌ������ł���B
�@���������āA�W���I�Ȓn���̌`�A���a�U�R�V�O�L���̋���(�����ȉ~�́j���l���āA���̕\�ʏ�
�̈ʒu�ł̋������l���Ȃ����Ƃ������ɂȂ�B
�@���R���ۂ̋����𑪂�ɂ́A��B�_�̈ʒu�Ǝ����_�̈ʒu�̍���(�W���j������B�܂��A��
����̕W���ς��A���ϕW���ł̐����ϑ��������o���A���̌㏀���ȉ~�̖ʏ�ł�
�����ɒ����A�k�ڌW���������鎖�ɂ�蕽�ʒ��p���W�ʏ�̋�����Ƃ��������ɂȂ�B
�@��x�u�`���ƁA���̎��͉������悤�ȋC�ɂȂ�̂��A���̓��e��Ək�ڕ�̊W��
����B�k�ڌW���ɂ��ẮA�|������A��������A�u�������ƁA���x�͊|����̂��A����̂�
�ȁB�v�ƂȂ�A���̒��ō������鎖���т��������B
�@�Ԉ���Ă������A�u�������̎��A�①�ɂ̗Ⓚ���Ă����Ԃ����ʒ��p���W�ł���B�v�Ɨ��\
�ɍl�����B
�@�ۑ����鎞�́A���̏�Ԃ̋Ȗʍ��W��Ⓚ����̂ŕX(�k�ڌW���j���|���ė�₷�B����
�āA�ۑ��������̂��A�g�p���鎞(�ΐS��̌v�Z���鎞�j�͗Ⓚ���Ă�����̂��𓀂��邽��
�ɁA���\�����X(�k�ڌW���j�������Đ��̏�Ԃɂ��Ďg�p����Ə���ɍl�����B���_�I�ɕ���
���l����Ȃ��Ȃ��Ă��钆�N�j�̔]�זE�ɂƂ��āA����������g�ł����Ȃ��Ɗo������Ȃ��B
���ǂ��������
�@�ϑ��̎��ۂɂ��āA�ӊO�Ȏ��ɁA�~���[�̒��S�Ŋϑ����Ă͂Ȃ�Ȃ��Ƃ����B�u�������낤�v�B
���̓s���|�[���ƃs���|�[���v���Y���Ńg���o�[�X���ʂ����鎞�A�K���v���Y���̒��S�Ŋϑ�
�������B
�@���g�����V�̖]�����Ŏ����_�̃v���Y����`���A�������܂��������ǂ����m�F���Ċϑ�����
�����B�u�~���[�̒��S���ʖڂȂ�A���Ⴀ�A�ǂ�������́v�B��X���g���o�[�X���ʂ�����ꍇ�A
�T�O���[�g�����x�ł���v���Y���̃N���̑��̂悤�ȁA�v���Y���̐�������A���S������₷
���̂ɉ��̑ʖڂȂ̂��A�����ς����Ȃ��B
�@�ׂ̑��ʂɏڂ����l�Ɂu�s���|�[���v���Y���ł͑ʖڂȂ́B�v�����Ɓu�S���ʖڂƂ�����ł͂�
��܂��A�v���Y���̒��S���{���ɁA���_�̒��S�Ȃ̂�����Ȃ��ł��傤�B������A���˔�
�̃}�[�N����������Ηǂ���ł��B���̓s���|�[���v���Y���p�̔��˔�t���Ďg�p���Ă�
�܂��B�v
�@�{�_�̍u�`�ł́A�u�������A�����p�ϑ��̎��ƁA�����p�ϑ��ł͔��˔̎�������}�[�N��
�ʒu���Ⴂ�܂��B�v�Ƃ̐���������B
�@�w�A�[�ŋ���Ŏ������鎖�ɂȂ�̂����A���Ŏ����ʒu�Ɣ��ł̖]�����̉�ʂł̎�����
�u��ɂ��Ȃ���Ȃ�Ȃ��B�Ƃ̐����̑O�Ɏ��̓w�A�[�ł͂��ނ��ƂȂǂ������Ƃ��Ȃ��A
�߂��ł���A�K���]�����̒��S�́{��̈ʒu�Ŋϑ����A�����������p�����Ŋϑ����Ă�
�܂��Ă����B
�@�X�ɁA�����̃|�[�����������鎞�́A��{���̃w�A�[�ŋ��܂��A��{���̕��̃w�A�[�ŏd
�˂�l�ɂ��āA�|�[���������l�ɂ��Ċϑ����Ă����B���R�A�|�[�����N���Ɍ������A�����ڂ�
���Ă���l�Ȏ��́A�w�A�[����͂ݏo���A�ǂ̕������{�̂̒��������f�����������A������
���A���̂����肾�낤�Ɛ��ǂ��Ă����B�܂��Ɏ��ȗ��̉�ł���B
�@�{���̊ϑ��ɂ��Ă͐}�̂Ƃ���
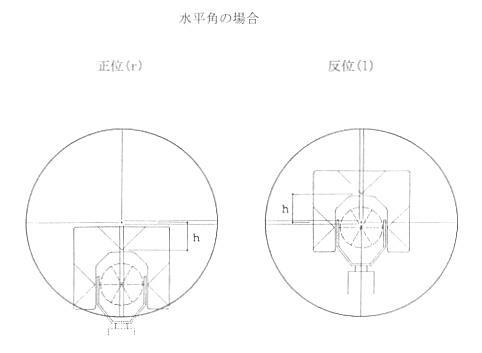
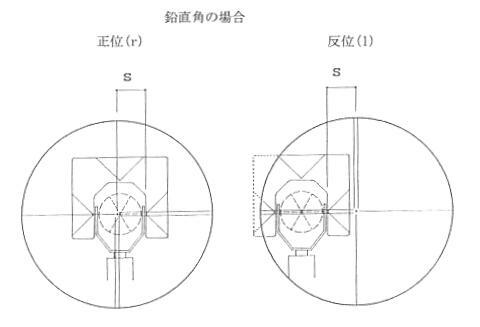
�����@��
�@�ϑ��̏��Ԃɂ��āA�����A�����p�A�����p�̊ϑ��Ƃ���̂����A��̂ǂ̂悤�ȏ��Ԃ�
���悢�̂��A�F�ډ���Ȃ��B
�@���̃g���o�[�X���ʂ̂����́A����̗v�̂Ńs���|�[�����g�p���A�s���z�[���v���Y����
���S���������A�����p�����������̏ꏊ�ň�C�Ɋϑ����Ă����B���̂��߁A���܂ɂQ�Ή�ϑ�
�̐^�������������ł��A�P�Ή�ڂ̐����p�̐��ʂ̊ϑ��̎��Ɏ������Q��ϑ����A���ʂ�
���ɓ������A�����p�Ɠ����Ɏ������Q��ϑ����Ă����B
�@��������ȗ��Ŋϑ����s���Ă��A���ʂ����o��Ηǂ����낤�A�����O�̂��ߕ����Ă݂悤�B
�u�����̊ϑ��Ɗp�x�̊ϑ��S��������ɂ���Ă������B�v�u�����A�ʖڂł��B�ϑ��̏�����S
������ɂ��āA�ϑ����Ȃ���Ȃ�܂���A�����͋����A�����p�͐����p�A�����p�͉�
���p�Ŋϑ����ĉ������B�v������A�ʓ|�������Ȃ��B�����A�u����������悤�ɁA�����A�����p�A��
���p�Ƒ��Č���ꏊ���Ⴂ�܂�����A�ʁX�Ɋϑ����Ȃ��ƁA�������Ėʓ|�L���ł���B�v�Ɠ{��
��B
�@��̊ϑ��Ŋ������̂����A��͂�ʁX�Ɋϑ����āA��������ł��ƁA�ϑ��̃��Y�����ǂ���
��A�����ɂ�����₷���A���ԓI�ɂ��قƂ�Ǔ���ł��鎖�����������B��͂�A���ȗ��ɗ���
�ꂸ�A��{�ɒ����ł��鎖����Ԃ̂悤�ł���B
���O�r�̐�����
�@�@�B�̍����Ƃ́A���_�̕W�̓��̍�������̍����ł���A�n�\�ʂ���̍����ł͂Ȃ��B��
���A�@�B�̍����������ʒu�ɂ��́A�@�B�̉��ɂ��Ă����B���}�[�N�̈ʒu�ł��鎖��
�����B
�@�@�B�̍������ɂ���A�����̕ΐS���l�������Ă��ǂ��̂łP.�S���[�g���Ƃ��āA�e�X�R��
�y�b�N�X�ō����𑪂�Ȃ���A�O�r�𐘂��Ă������A�P���ɎO�r�����Ă邾���ł���A�����b
�����Z���݂�Ƃ���ȒP�ɂ������̂����A�����͋@�B�̍������P.�S���[�g���ɂ��Ȃ����
�炸�S������ꓬ���Ă���B�ق�̂�����Ƃ������ŁA�����������ς��A���_�̈ʒu����O
��Ă��܂��B
�@����ƁA�o�����Ǝv���A�@�B����ɏ悹��ƁA�˂����g�p���āA�O���猩�Ă����炩�ɁA�@�B
���X���Ă��܂��Ă���l�ɂ݂��鐘���t�����ɂȂ�����B�O�r�����炭�A���тȌ`�̎O�p�`��
�Ȃ��Ă����肷��B
�@����ł��A���Ƃ��A���������B
�@�����ϑ����A�N�����H���Ă��鎄���ŏ��Ɋϑ����鎖�ɂȂ����B���������p����ϑ����鎖
�ɂȂ�̂����A�����̎g�p���Ă��郁�[�J�[�̂��̂łȂ����߁A�˂��̏ꏊ����ߕt��������
���Ⴕ�āA�Ȃ��Ȃ��X���[�Y�Ɋϑ����o���Ȃ��B����Ɗϑ����I���������A�ǂ����ϑ��l����
���ł���B�u������A���������ȁB��B�������̂��ȁB�v
�@�����̘r�̈�����I�ɗg���āA�����̕��ɁA�u�ǂ����A��B��������Ȃ��v�ƌ��疳�m��
�����ƁB�u���̂��A���̊�B�����Ɛ����t������Ă��܂����B�ǂ����A�C�A�ǂ̋C�A�͍����Ă�
�邩������܂��A�����ڂɂ���B�����тɂȂ��Ă��܂���B�v�X�ɁA�u�O�r�A�ǂ����ݍ���
��Ă��܂����B�v
�@�u�������A����Ȏ��W����́v
�@���������A���炩�Ɍ��g�����V�̂˂����O���Ƃ��������Ⴄ�B�X�ɁA�l�̊�B�ׁ̈A��
�̔얞�̂��C�ɂ��āA�y�����ݍ����x�ł������B
�����̎����̎d���Ԃ肪�o�Ă��܂��B���ȁB
�@�Ȃ��A�ŋ߂̌��g�����V�ɂ͌X���������ŕ����悤�ɂȂ��Ă���A���̌X����\������
�l�ɂ��Ȃ��Ă���B��x�����������t������B���ǂ̒��x�X���Ă��邩�m���Ă����Ă��ǂ�
�̂ł͂Ȃ����낤���B�ĊO�������v���Ă�������X���Ă�����̂ł���B
�����E���ƃV�t�g��
�@����͂T�p�`�̃g���o�[�X���ʂł��邽�߁A�����Ȃ�T���_���ĂɎO�r�𐘂��āA���E����
���˔ƌ��g�����V�̓������𐘂��t���ς��Ă̊ϑ��ƂȂ����B
�@����ł���ƁA���S�ɂ��ẮA��x���S���Ă����ƁA���̌�́A�����t���ς��邾���ŁA��
�Ԃ���炸�ȒP�Ɋϑ����o����B
�@�S�������͂��Ċϑ����邽�߂ɂ͂�͂蒅�E���ł����������ǂ��B���g�����V�┽�˔Ղ�
��Ղ��������O���A���̂܂��ւ��邾���łǂ�ǂ�ϑ����鎖���o���A���Ԃ̐ߖ�ɂ�
��B
�@���̋@�B�͎c�O�Ȃ���V�t�g���ł���B
�@�J�Ɠ����ɁA�Ǝ҂Ɂu�y�n�Ɖ������m����́A�Q�O�b�ǂ݂ŏ[���ł���B���S����ɂ�������
�V�t�g���̕����ȒP�ł���B����ɂP�O�b�ǂ݂��ƂQ�O���ȏ㍂���Ȃ�܂���B�v�ƌ����A����
���܂܂ɔ����A���낢��ȕt���i�������A���g�����V�̔����ς��ɂ������Ă��A�P�O�b�ǂ�
�̊�B�ɂ͂����̂����A�����i�Ƃ̗��݂���A���܂��ɃV�t�g�����g�p���Ă���B
�@���̂��ߍŏ����璅�E���ɂ��Ă����Ηǂ������Ǝc�O�Ɏv���Ă�
��B
�@�������A�u�V�t�g���ł����Ă��A�P�O�b�ǂ݈ȏ�̋@�B�͂Q���o�܋V�ł�����A���Ȃ��̋@�B��
�Q���o�܋V�ł���B�����@�B�Ȃ�ł�����B�ǂ�ǂ�g���ĉ������B�v���Ƃ��ẮA���g������
�����̂����A�������S���鎖���o�����B
�@�������A����̐V�l����ɂ́A���̂悤�ɂȂ�Ȃ��ׂɂ��A����Ƃ��P�O�b�ǂ݈ȏ�̒��E��
�̌��g�����V��E�߂������̂ł���B�ŏ�����ł�����[�X�̗����̒lj��z���m��Ă�
��B������x�����Ă��܂��ƁA���̍��z�����̒Nj��ł͊�B���������Ă���Ȃ����A�܂�������
���������̂������ł��낤�B
���Q�Ή�
�@����̊�_���C�ɂ��ẮA�S����_�̍�ƋK��Ō��C���s���Ă���B���������Đ�
���p�͂Q�Ή�A�����p�͂P�Ή�A�����͎������Q�Z�b�g�Q��̊ϑ��ł���|�̐���������
���B��X�����m�͂Q�Ή�Ƃ����������Ȃ��A���������g���o�[�X���ʂł����Ă����Ή��
�ϑ����Ă��̂܂܂ɂ��Ă���ꍇ�������B
�@���ʂ̊ϑ��ł���A���i�̂Ƃ���̊ϑ��ŗǂ����A�P�W�O�x��]�����]�����A���ʂ̊ϑ�
�ł���B�ŋ߂̌��g�����V�͔��]���Ă��A���Ε����ł��A�f�W�^���\������邽�߁A�ǂݎ��
���̂͊ȒP�����A�˂��͑��āA���܂킵�ɂȂ�A���A�����p�̒����˂��̈ʒu�͊��S��
���Α��ɂȂ�B
�@�܂��A�Q�Ή�ڂɂ��ẮA���]�����ʒu�ł̊ϑ��ł���A�Q�V�O�x����̐����p�ϑ����n��
�鎖�ɂȂ�B����́A�ŏ��̐��ʂł̂P�Ή�ڂ̊ϑ��͂O�x�֊s�A�����ĂQ�Ή�ڂ͂X�O�x��
�s�ŊJ�n���邽�߂ł���A��B�̂��ڐ���̌덷��������ʒu�̖ڐ�����g�p���鎖�ɂ�
���āA�덷���������邽�߂ł���Ƃ̐���������B
�@���̐����͕�����̂����A���̂Q�Ή�ڂ̍ŏ����Q�V�O�x����n�܂�̂��s���Ɨ��Ȃ��B
�@����͂Q�Ή�ڂ͔��]�����ʒu�ł͂��܂邽�߁A�X�O�x�̗����̈ʒu�͂P�W�O�x���������p�x
�ƂȂ�Q�V�O�x�ɂȂ�Ƃ������ł���B
�@�R�Ή�̏ꍇ�́A�P�W�O�x���R�Ŋ������l�̂O�x�A�U�O�x�A�P�Q�O�x�̗֊s�Ŋϑ����邪�A����
����̑Ή�̍ŏ��Ɋϑ�����p�x�͂P�Ή�ڂ͐��̈ʒu�A�Q�Ή�ڂ͔��ʂ����ĂR�Ή�ڂ�
���ʂƂȂ�A���ꂼ��ϑ����J�n����p�x�͂O�x�A�Q�S�O�x�A�P�Q�O�x�ł��ꂼ��J�n���鎖��
�Ȃ邻�����B
�@���g�����V�̏㕔�Œ�˂��Ɖ����Œ�˂������ꂼ����߂Ċp�x�����킹�Ċϑ����J
�n����B
�@�����A�Q�Ή�ϑ����s�����ۊ���Ă��炸�A�����Œ�˂�����������Œ肹���ɁA�ϑ����A�P
�Ή�ڂ̊ϑ��l�ƂQ�Ή�ڂ̊ϑ��l���Ƃ�ł��Ȃ��l�ƂȂ��Ă��܂������C���������悤�ł�
��B
���{�p���A�ϑ���
�@�����p�ϑ��̂Q�Ή�̊ϑ������������ǂ����A���̐����Ƃ��āA��������ւ̊ϑ��p�̂P��
��ڂ̊ϑ��p�̍��v�l�i���{���j�ƂQ�Ή�ڂ̊ϑ��p�̍��v�l�̍���{�p���Ƃ����B
�@�X�ɁA���x�͂P�Ή�ڂ̐��ʂł̊ϑ��l�Ɣ��ʂł̊ϑ��l�̍�(���|���j�ƂQ�Ή�ڂ̓�����
�̊r�����ϑ����Ƃ����B���ꂪ�S����_�ł͂R�O�b�ƂQ�O�b�̐����ł���Ƃ����B
�@�����A�ϑ�����s����Ȃ�A���҂�����ɗւ��������悤�ȏ��S�҂ł��邽�߁A�ϑ��肪
�ϑ��l��ǂݏグ��ɂ�������炸�A���̊ϑ��l�����Ȃ���A�}�X�ڂɐ�������������
�̂ɐ���t�ŁA�����̐����̈ÎZ���o���Ȃ��B����ǂ��납�A�㎋�_�̊ϑ��̒l��������
���āA�ϑ��p���Z�o����ɂ��A�x�A���A�b�̊��o�Ɋ���Ă��炸�A�Ȃ��Ȃ��v�Z���o���Ȃ��l
�ł���B�Q�Ή�̊ϑ����I�������ɂ�������炸�A���҂́A������{�p���A�ϑ����̌v�Z
�ɂƂ肩���낤�Ƃ��Ă���B
�@�d����g�p������A��l�|��ł���ƌv�Z�A���̋����傪�������ɓ��炸�đ��ƂȂ�A����
�̂����鎖�B
�������p
�@�����p�ɂ��ẮA���X�ł���B�P�Ή�Ȃ������������A�g���o�[�X���ʂ��s�����ł��A
�ʓ|�L���Ɖ����p���ϑ������A�����Ȃ萅�������𑪋�����݂̂Ƃ��A�O�̂��߁A�O�������A
�㎋�����ƂȂ������ɁA���������Ȃ炸����������ϑ����Ď����Ȃ�̏���Ȕ��f�Ŋr����
�R�����ȓ��Ȃ�n�j�Ƃ��Ă����B
�@�]���āA�����p�̐����ϑ��̂P�Ή�Ƃ������ɂȂ�ƁA�����p�ϑ��̎��̂悤�Ɋr���̐���
�Ƃ��������̂��ǂ��Ȃ̂��A�ǂ��������_���̎d��������̂�����Ȃ��B
�@�X�ɂ͂��̂P�Ή�ϑ��̕��ϒl�̏o������������Ȃ��B�P���ɍl����ΐ��̊p�x�Ɣ��̊p
�x�𑫂��R�U�O�x�ɂȂ�͂�������A���̊p�x�����ł�������Ȃ��́B�ƒP���Ɏv���Ă�
�܂��A�����p�̊ϑ������ʂȗl�Ɏv���Ă����B
�@���̂��߁A����������A�����������ϑ����A���̊r���ŗǔۂf���Ă����B
�@�����A���ۂɊϑ����Ă݂�ƁA
�@�@�@�@�@�@���i���j�@�X�O�x�O�W���T�O�b
�@�@�@�@�@�@���i���j�Q�U�X�x�T�O���T�T�b
�@�@���{���i���{���j�R�T�X�x�T�X���S�T�b
�@�Ƃ����A�ӊO�Ȍ��ʂɂȂ��Ă��܂��B�����p�̊ϑ��Ȃ�A�قƂ�ǂR�U�O�x�ɂȂ�͂��Ȃ̂�
�Ǝv���Ȃ���A���ȊO�̊ϑ��҂ɂ����Ă��قƂ�Ǔ���̌��ʂł������B
�@���̎����ɋ����ƂƂ��ɁA���A���̊p�x���������p�x�ƂR�U�O�x�Ƃ̊r���������ɂȂ�̂���
�v���Ă������A�_���̂��߂ɂ����P�����̉����p�𑪂�A���̐��A���̊ϑ��p�̍��v�l���m
�̊r���������ɂȂ�Ƃ����B��������x�퐔�Ƃ����B���̌��t������̌��C�Ŏn�߂Ēm�����B
���̍��x�萔�̉����p�̊r�����R�O�b�������ł���Ƃ����B
�@�܂��A�n���̊ۂ��̌덷���������邽�߂ɁA�o������A�����p���Ɋϑ����A���̕��ϒl
���Ƃ�A����������������@������炵���B�ǂ�����X�͒n���K�̘͂b�ɂȂ�ƃs���Ɨ��Ȃ���
��B
���ÎZ
�@�܂��A���̉����p�̕��ϒl�̏o�������ǂ����ÎZ�ɂ͕s�����Ȍv�Z�ł���B���ϒl�����߂�
���߂ɁA�Q�y�����|���@�̌v�Z�����āA�X�O�}�����y�@�ƂȂ胿�̒l���o���Čv�Z�I���ƂȂ�̂�
���A���ꂪ�Ȃ��Ȃ��ÎZ���o���Ȃ��B�܂������p�̌v�Z�ł���A���Ƃ��v�Z�ł���̂�
���A���̉����p�����́A�͂Ȃ���R�U�O�x�������Ȃ��ƌv�Z�o���Ȃ��B��L�̗Ⴞ�ƁA
�@�@�@�@�@�Q�y���X�O�x�O�W���T�O�b�|�Q�U�X�x�T�O���T�T�b
�d���Ȃ��A���̌��ʂɂR�U�O�x��������
�@�@�@�@�@�Q�y���@�X�O�x�O�W���T�O�b�|�Q�U�X�x�T�O���T�T�b�{�R�U�O�x�ƂȂ�
�@�@�@�@�@�Q�y���P�W�O�x�P�V���T�T�b
�@�@�@�@�@�@�y���@�X�O�x�O�W���T�V�b�T�ƂȂ�l�̌ܓ����ĂX�O�x�O�W���T�W�b
�@����ɂX�O�}�����y�ł��邩��
�@�@�@�@�@�@�����|�O�x�O�W���T�W�b�ƂȂ�
�@���̈�A�̌v�Z���ÎZ�ł��Ȃ���Ȃ�Ȃ��B
�@�����ł����������Ă���ƁA�u�����p�̂��{���͊ȒP�Ɍv�Z�o����ł��傤�B���̒l���R�U�O�x���
��������̉����p�ɂ��̉z�����p�x�̔�����������������B�t�ɏ��Ȃ���Ώ��Ȃ��p�x
�̔��������̉����p�ɉ�����A�y�̒l�͏o�邵�B���ꂪ������A���͂X�O�x����������
�X�O�x����z�����p�x�̕����}�C�i�X�̕\���ɂ���悢�B�t�ɂX�O�x��菭�Ȃ���X�O�x
���s������p�x���v���X�\�����������ł���B�v�ƍu�t�̓{�鐺����������B
�@�����ł̗Ⴞ�Ƃ��{�����R�T�X�x�T�X���S�T�b�͂����ɈÎZ�o����B
�@�X�ɂ��̊p�x���R�U�O�x���P�T�b�s�����Ă���B���������ĂP�T�b�̔����̂V�D�T�b�������p
�̂��̊p�x�X�O�x�O�W���T�O�b�ɉ�����ƂX�O�x�O�W���T�V�b�T��������A�b�ȉ����l�̌ܓ�����
��A�X�O�x�Ƃ̍����l���A�V�����O�x�ł��邩��X�O�x�ȏ�ł���Ή������̕����ɂȂ�}�C�i
�X�\���ƂȂ�B���������ă����|�O�x�O�W���T�W�b���ȒP�ɓ��鎖���o�����B
������
�@�������������ϑ��������̖������ɂƂ��āA���g�����V�̃{�^�������������������̂�
���͂��Ă��邽�߁A�{�^�����삪�ʓ|�L���Ƃ������R�ŁA�����𑪂������̖������́A�ϑ�
����x�ɊԈ���Đ��������𑪋������̂ł͂Ȃ����ƕs���ɂȂ�A���g�����V���āX�`����
�ށB
�@�O�r���g�p���Ĕ��˔ƃ~���[���g���Ċϑ��ȂA�قƂ�ǂ����A�s���|�[���ƃs���|�[��
�v���Y�������g�p�������̂Ȃ��������������́A�Q�Z�b�g�̋����̑���A�܂�S��̋�����
��ɂ�����炸�A�����̂�����قƂ�ǖ����Ƃ������B�܂��A�s���|�[���̊ϑ��̏ꍇ�A
�X�����ǂ����Ă�����A�X�ɓ���̋����ł����Ă��قȂ��������̊ϑ��ł���A�ǂ����Ă�
���������A����̃Z�b�g�ł����Ă��Q�A�R�����̂�����o�����Ă��鎄�ɂƂ��āA���炭
���S����������B
�����S�]����
�@�����A���̎O�r���g�p�������ʂɂ��v��ʖӓ_������ƌ����B�ʂ����ċ��S����������Ȃ���
�Ă��邩�ǂ����B
�@��_���ʂ̌��C�ɂ������āA���S�ɂ��Ă͐������g�p���Ȃ����Ƃ������ӂ��������B��
�����Ȃ���A�����A������B�𐘂��t�����o���鎖���������Ă��钲���m�Ɍ����Đ������g�p
���������Ȃ��A���S�]�����ŋ��S�����Ă���B����ɍs���A�y��������u����ȓ���Ƃ���
�ɁA�����U����g�킸�ɁA�悭��B�����Ă��Ȃ��B������������P�O���ȏォ���邺�B�v�ƌ���
�ꎩ�����Ɍ��g�����V�����Ă��o���͂P�x��Q�x�ł͂Ȃ����낤�B
�@�u�����U����g�������Ȃ������Q�A�R�N�������v�ƌ����Ȃ���A����ł��u�t���������߁A�F�A
�����U����g�p���ċ��S���Ă����B
�@��B��ݒu�B�����U��Ƒ��_����v�����̂��m�F��A�����̕ȂŁA���������B�̋��S��
�o���Ă��邩�ǂ������S�]������`�����ށB�u������B����Ƃ邺�B�v�Ȃ�ƁA�O�D�T�~�����x����
�Ă���B����̌��C�ɂ������ẮA���ʋ@�탁�[�J�[�̋��͂ŁA��B�̒����������������̂�
�g�p�������������B
�@�O�D�T�~�����x�ł���A�����U��Ƌ��S��ڂŊm�F���Ă�������Ȃ����x�ł��邪�A������
�����s���Ă��Ȃ��A��X�̊�B�ł���Ƃ��Ȃ�̂��ꂪ�������댯�������邻�����B����
�����m����̊�B�͂T�~�����̑��Ⴊ�����������ł���B
�@�������肵���g���o�[�X���ʂ������ɂ�������炸�A�v�����l�Ȑ��x�������Ȃ��ꍇ�B����
�ȂƂ���Ɍ���������̂ł́B�F�����x�A�_�����Ă����Ă͂������B
����@��
�@���ɂ��āA���̋L���ɂ��Ă̓y�����{�[���y���Ƃ������ӂ�����ɂ�������炸�A��
�Z���o���Ȃ��B�L�ڂ̎d���Ɏ��M�������Ƃ������R����A�قƂ�ǂ̕������M�ŋL�ځB����
�͂�������A���������S���ŏC���������������悤�ł���B
�@�u�`�̒��ŁA�K���C���N���{�[���y���łƌ����A��肪����ꍇ�͕K���C����������悤
�ɂ��Ē������鎖�ƌ���������ꂽ���A��͂肻���͓y�n�Ɖ������m�ł���B�n�ϑ��ʐ}�͌�
�J���Ă��邪�A���̎������ɂ��Ă͌��J�����o���̖����҂��قƂ�ǁB�ŏ��̖쒠����A
���q����Ɍ�����Ƃ�����������A�����������萮�����ēn���K�v������B���R�A��_
���ʂł���Ό����@�ւɒ�o���āA�������Ȃ��Ȃ�Ȃ��B��͂�A��X�̑��ʂ͈�
�l�悪��ȑ��ʂȂ̂��낤���B
�@�܂��A���ɂ́A�K���n�܂�̎��ԂƏI���̎��Ԃ̋L�ڂ��K�v�ł���B�ϑ����Ԃɂ���
�����������鎖�������Œm��B��ŏ����̕��ɁA�u�{�ɂ͊ϑ��̎��Ԃɂ��Ă̐����͖�����
���l�ł���B�v�ƕ����Ɓu�{�ɂ͖��������m��܂���ˁB�ł�����͑��ʂ̏펯�ł���B����ς�
�K���Ȏ��ԂƂ������̂�����܂���B�v
�@�X�ɁA���͓��R���҂��ϑ��҂̊ϑ��l�����Ȃ���L�ڂ��A�L�ڂ����l��v�Z�l��
�`�F�b�N���s�����A�K����ŁA�����ɂ��đS���ϑ��҂��`�F�b�N���Ȃ���Ȃ�Ȃ�������
����B��d�A�O�d�Ƃ���������̔r���Ɋ��S������B
�@���́A�p�������Ȃ��猻�ݎg�p���Ă���g�����V�b�g�쒠�����A���̐����ȋL�ڕ��@��m��
���A���S�Ɏ��ȗ��ŋL�ڂ��Ă���B���R�A����ɉ������̎�������A���̖쒠�ɋL�ڂ���
�����A����̂��߂̎Q�l�ɂ����Ă���̂����A�ʂ����āA���ȊO�̐l�Ԃ����̖쒠���݂��Ƃ�
�ɓ������������邾�낤���B�X�ɁA�������������ꂽ���A�����g�������o����ł��낤���B
�@���̎��̐������ꂽ���ڂ��݂Ȃ���A���͍l������Ȃ��B
���W�@��
�@���e�������ɂ������āA���ϕW�����v�Z����K�v������B�n���̔��a�U�R�V�O�L������
���Ƃ��āA���̏ꏊ�A�܂�W���ɂ������������\���������قȂ邽�߁A����̋����ɂ���
���߂ɂ́A�ϑ��_�Ǝ����_�̕W����m��A���̕W�����Q���̂P���鎖�ɂ��ϑ������̕�
�ϕW����������A�m�蓾�����ϕW���������ȉ~�̏�̕W���Ƃ��āA�ϑ����������͖{���ɂ�
����Ȃ̂����Z�o���Ȃ���Ȃ�Ȃ��B
�@���R�A�����Ȃ�{���̕W�����������ł͂Ȃ��A�T�Z�l�ł���B�^�_�̊��m�̕W�����獂�x
�p�Ƌ����ō��፷���v�Z���A�����Ƃ���_�܂ł̕W�����v�Z����B���̌v�Z���s�Ȃ����Ɋ�
�B������v�����Ă����ƌv�Z���y�ɂȂ�Ƃ����������������B
�@��X�����m�ɂƂ��āA�����Ƃ������͂��܂�C�ɂ������������̂��{���̏��ł���B���X�A
�f�ʐ}�ɍ��������Ă���Ƃ��A����Ȏd���ŕW�������鎖�͂��邪�A�����g�����g����
�V�ō������Ƃ��ėǂ��̂��낤���ƕs���ɂȂ�A���g�����V�ƃ��x�����Ȃ�ׂāA�s���|�[����
�X�^�b�t�����݂Ɏg�p���Ă̍������Ƃ����肵�Ă���B
�@�����A���̌��C�̂������ŁA���J�ɍ��x�p�����Ƃ�Ώ[�����p�o���鎖���킩��B
����B�̕�
�@�ϑ����I�����A�v�Z�̂��߂Ɍ��C���ɖ߂�ƍu�t����A�u�S���ϑ��͏o���܂������B�v�ƘJ��
�̌��t�̌�A�u����ł�������_�����o�����ɁA���ꂩ��A��v�Z��������A�ǂ����ϑ��̒l��
���������B�������z���Ă���A�{���͍đ������Ɍ���ɍs���Ȃ���Ȃ�Ȃ����A���̂�����
�R�̒��Ȃ��Ƃ�����x�s���̌����B�Ƃ������Ŋϑ��̒l��ς��Ă��܂��l�������肵�܂�
���A����͐��Ƃ�����Ƃ����킩���ł���B�v
�@�����A�u���̃f�[�^�ǂ������������ȁA�r���̐������z���Ă��܂����A�ǂ����A���̑Ή�̂�����
���������ȁA���̒l�������킾������A�܂Ƃ��Ȃ̂ɁB���������A�P�O�b���A�k�߂Ă��܂��v�ƈ�
���ɍl�����肵�Ă��鎄�ɂƂ��Ďv�킸�h�L�b�Ƃ���悤�Ȍ��t������B
�@�b�ɂ��ƁA����ϑ��̑Ή�̒��Ő��ʂƔ��ʂ̊ϑ��l�͊�B�̕ȂŁA�ǂ��炩�̒l����
�ɑ傫���Ȃ�Ȃ�����炵���B���������āA�P�Ή�ڂ͐��̒l���A�Q�Ή�ڂ͔��̒l���傫����
�鎖�͖����炵���̂ł���B����Ȏ��͎n�߂ĕ����b���B�������g�̍��܂ł̊ϑ��ŁA�����
�ɋK���I�Ɋϑ��l���ω��������͖����B���ɍ���̊ϑ��l���݂Ă݂Ă��A�S���o���o���ł�
��B
�@�u�t�̌�����A�u��B�̕ȁv�́A�����萅���ȏ�̐l�����������B�𐘂��Ċϑ�����
�ꍇ�ɂ����鎖�ł���炵���B���������ĉ�X�͂��̐����܂ŁA�y���ɋy��ł��Ȃ��B�����m
��������̑��ʂ̕���̐��Ƃł��邽�߂ɂ́A���Ȃ��Ă���B�̕Ȃ����钲���m�ɂȂ�
�������̂ł���B
�����W�v�Z
�@�ϑ��������ʂɂ��A��x�J���g���o�[�X���ʂ̗v�̂Ŏ��ۂ̊ϑ��p���g�p���A���m�̕�
���p������t���̕����p�܂ł������v�Z���čs�����m�̎��t�������p�Ƃ̍����r�B��
�R���������邪�A��X�̃g���o�[�X���ʂ̕����Ƃ͑S�R�قȂ鍷�ł���B�T�ϑ��_�ŕ���
�����Q�O�b���x�ł���A���܂ł͂܂��܂��̐��x���Ǝ����ł͔[�����Ă����̂����A�ǂ���
���̒��x�Ŗ������Ă����̂ł͂����Ȃ��炵���B
�@����͌��C�Ƃ�����������A�����̕����ق��Ă��Ă��ꂽ�l�ł���B�@
�@�������ɂ���Ό덷�̔z�z���Ȃ��낤���A�����낤�������ł���B��芸�����e�ϑ��_�ւ�
�덷�̔z�z�ɂ��āA�����e�ϑ��_�̐��Ŋ���A�o�ė��������ɂ��Ă͂��̂܂܁A�e���_
�ɔz�z���A�c��̗]��̐��ɂ��Ă͓K���ɔz�z����Ηǂ��A�m���S�T�x�ɋ߂��l�̏��ɔz
�z����Ηǂ��Ƃ����悤�ɖ{�ł��ł����̂����A�ǂ�������͎��������o���Ă����悤�ł�
��B
�@�������͈ȉ��̂Ƃ���炵���B
�@�덷���ϑ����Ŋ���A��ʁi�����_�ȉ��j���o���B
�A��Ԗڂ̕�ʂ͂��̂܂����_��P�ʂ��l�̌ܓ����A�m�肷��B
�B��Ԗڈȍ~�̊ϑ��_�ɂ��Ă͏����_�ȉ��̒l����������ʂƂ��̊ϑ��_�̏��Ԃ��|
�����l�ɂ��Ďl�̌ܓ����A�Y���ϑ��_�܂ł̕���̑��a���������Ƃɂ��A���̊ϑ��_��
��l�����肳���B
�@����ŁA�p�x�i�����p�j���m�肵���B���x�͋����ł���B
�@�m�肵���A�����p�ƒ��p���W�ʏ�̋������g�p���āA�������W���v�Z���Ă����Ɠ��l�Ɋ��m
�_�ł�����t���_�Ƃ̍��W�̍���������A������p�x�Ɠ��l�ɂw�����A�x�����Ɍʂɕ
���ċߎ����W�����肳���B
���d�@��
�@�ȏ�̌o�߂�d��Ōv�Z���Ă����̂����A��X���d��Ɋ��҂��Ă��鎖�͎l�����Z�̂�
�ŁA�ڂ����@�\�A���Ƀ������[�@�\�Ȃ�đS���g�p���������Ȃ��B�P�O�O�߂��@�\����������
�d������̎g�����������炸�A�܊p�̑��@�\��������L�[�������Ă��܂��A���̉����Ɉ���
�ꓬ���ז��ɂȂ��Ă��܂��Ă���B
�@�戵���������ȂA�u��������Ȃ��B�v�Ɠǂ܂��ɂ��ݔ��ɒ��s���Ă���B���̂����܂����Z
�p�v�V�ɂ��A���̋@�\���g�p����Ό��Ȃ��ȒP�Ɍ��ʂ��o����ɂ��ւ炸�A��X�͂����
�P�Ȃ�s������������Ă��܂��Ă���A�p�\�R���̑��ʃ\�t�g�Ɋ���Ă��܂��������m�A�u�O�H
�̒����m�v�Ȃ̂����m��Ȃ��B����ő��A���ɗ��d��A���ꂪ����ɂ��ւ炸�g�p���Ă���
����X�B�g�p���Ȃ��̂��B�o���Ȃ��̂��B
�@�����Ɍ����Ǝ��͌���ő����ɓd����g�p�o���Ȃ��B���̋@�\�ɂ��Ă͉��Ƃ��킩��
���A�g�p��������A�I�m�Ȕ��f���o���������A�ǂ����Ă��������ɋA��A�p�\�R���̉�ʂ��݂�
����łȂ��Ɣ��f�����˂�B
�@�T�d�ƌ����邩������Ȃ��B�������A��X�͋Z�p�҂ł���A�v���ł���B�܊p����őΉ�����
���̏o���铹�����Ȃ���A���̓�����g�����Ȃ��Ȃ��Đ^�̋Z�p�҂Ƃ͌����Ȃ��B
| |
  |
| |
|
|

